1. Изчертаване на равнинни криви

В случай, че кривата, която искаме да изчертаем, е зададена с уравнение от вида y = f(x), можем да използваме командата

Plot[f,{x,xmin,xmax}].

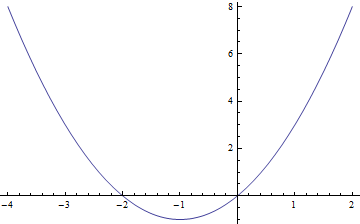
В къдравите скоби “{}” след уравнението на кривата първо се посочва буквата, с която е означена променливата и интервалът [x_min,x_max], в който тя се изменя. Например, ако искаме да построим графиката на параболата y = x² +  2x за стойности на x в интервала [-4,2], командата, която използваме, е

Plot[x^2+2x,{x,-4,2}]. 

След натискане на Shift+Enter, получаваме

За крива, зададена чрез векторно-параметричното си уравнение r = r (x(t),y(t)), където t е реален параметър, използваме командата

ParametricPlot[{x(t),y(t)},{t,tmin,tmax}].

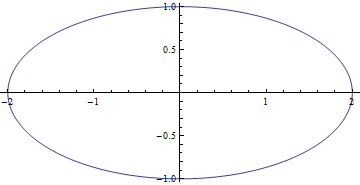
Координатните фукции x(t) и y(t) на радиус-вектора на кривата се разделят със запетая и се ограждат в “{}”. След тях се изписва интервалът на изменение на параметъра t. Например, за изчертаване на елипсата r = (2Cos t, Sin t) с неявно уравнение x²/4 + y² = 1, използваме командата

ParametricPlot[{2Cos[t],Sin[t]},{t,0,2Pi}].

Забележете синтаксиса на вградените в Mathematica функции – изписват се с главна буква, а аргументът им се загражда в квадратни скоби “[]”. Още примери от страницата на Wolfram.

В някои случаи е по-удобно са се използват полярни координати, вместо декартови (дотук използвахме декартови). Нека си припомним, че полярните координати на точка в равнината са ρ – дължината на радиус-вектора й (разстоянието от точката до началото на координатната система) и θ – ъгълът (мерен в радиани), който този радиус-вектор сключва с положителната посока на абсцисната ос. Тогава на лице е следната зависимост между декартови координати (x,y) и полярни координати (ρ,θ): x = ρ cos θ, y = ρ sin θ.

Ако кривата е зададена с уравнение от вида ρ = f(θ), командата, която можем да използваме, е следната

PolarPlot[f,{t,tmin,tmax}] (за удобство сме заменили θ с t).

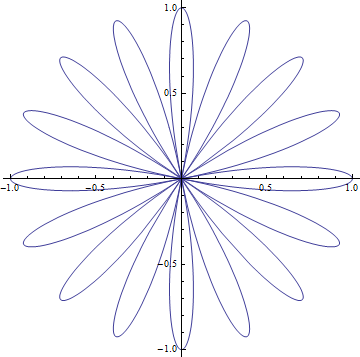
Едно интересно семейство криви, чиито представители обикновено се задават в полярни координати, са розите (на англ. език rose curves или rhodonea curves). Дефинират се с едно от уравненията ρ = cos (kθ) или ρ = sin (kθ). В случай на цяло и четно k, броят на венчелистчетата е 2k (за стойтости на θ в интервал с дължина 2π) , а за цели и нечетни стойности на k, броят на венчелистчетата на розата е k (θ се изменя в интервал с дължина π).

За да изчертаем роза с 16 венчелистчета, използваме командата

PolarPlot[Cos[8t],{t,0,2Pi}].

Роза

На страницата на Mathworld на Wolfram можете да разгледате какви “цветя” се получават за някои “по-екзотични” стойности на k, например за k = e, π  и т.н.

2. Изчертаване на пространствени криви

За пространствени криви, зададени с векторно-параметрично уравнение r = r(x(t),y(t),z(t)), използваме командата

ParametricPlot3D[{x(t),y(t),z(t)},{t,tmin,tmax}].

Ето пример с витловата линия (helix на англ. ез.)  r = r(cos t, sin t, t/2). За да изчертаем частта от кривата за стойностти на t в интервала [0,4π], изпълняваме

ParametricPlot3D[{Cos[t],Sin[t],0.5t},{t,0,4Pi}].

Витлова линия

От тук можете да изтеглите файла (Mathematica notebook, .nb) с горните примери.

Следва продължение…